Embark on an enlightening journey into the realm of geometry as we delve into Unit Plane Geometry and Similarity Homework 8 Answer Key. This comprehensive guide unlocks the intricacies of unit plane geometry, empowering you to conquer geometrical challenges with precision and confidence.
Delving into the fundamental concepts of points, lines, planes, and angles, we unravel the practical applications of unit plane geometry in our world. Moreover, we explore its profound connections to other mathematical disciplines, illuminating the interconnectedness of knowledge.
Unit Plane Geometry Concepts
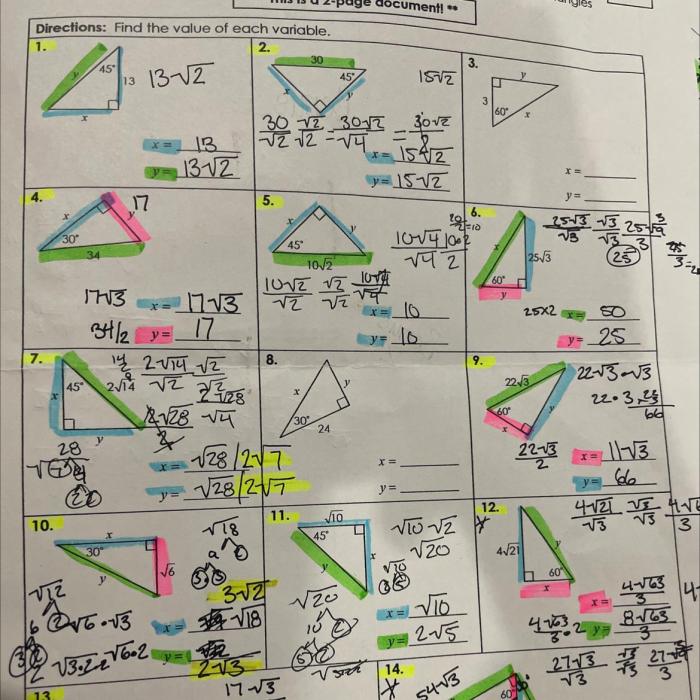
Unit plane geometry is a branch of mathematics that deals with the study of points, lines, planes, and angles. It is a fundamental subject that provides the foundation for more advanced topics in mathematics, such as calculus and trigonometry.
Points are the most basic elements of unit plane geometry. They are considered to be dimensionless and have no size or shape. Lines are one-dimensional objects that extend infinitely in both directions. Planes are two-dimensional objects that extend infinitely in all directions.
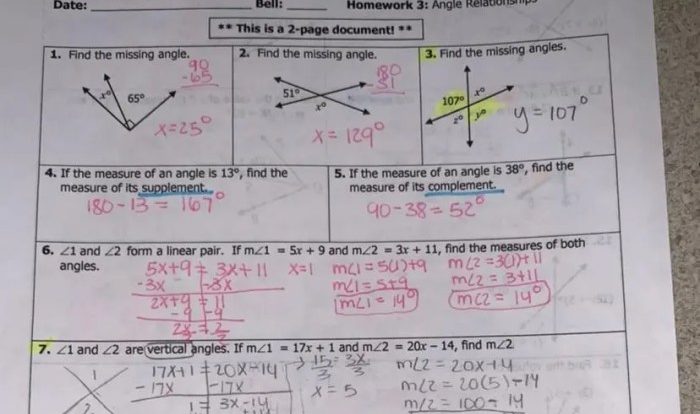
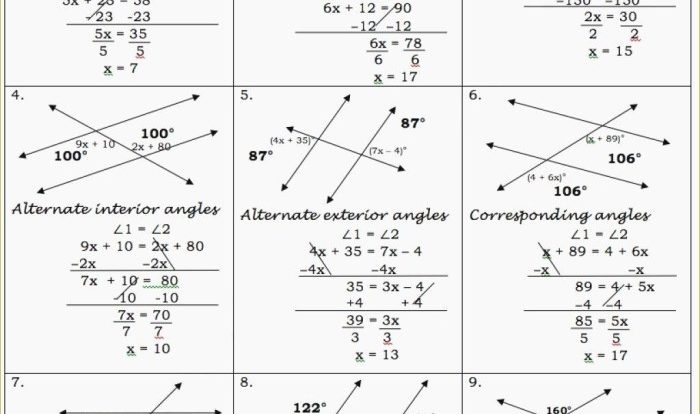
Angles are formed by two lines that intersect.
Unit plane geometry has many applications in the real world. For example, it is used in architecture to design buildings, in engineering to design bridges and other structures, and in navigation to determine the best route to take.
Unit plane geometry is closely related to other branches of mathematics, such as algebra and trigonometry. Algebra is used to solve equations and inequalities that involve geometric objects, and trigonometry is used to study the relationships between the sides and angles of triangles.
Similarity in Geometry
Similarity in geometry is a relationship between two figures that have the same shape but not necessarily the same size. Two figures are similar if they have the same angles and their corresponding sides are proportional.
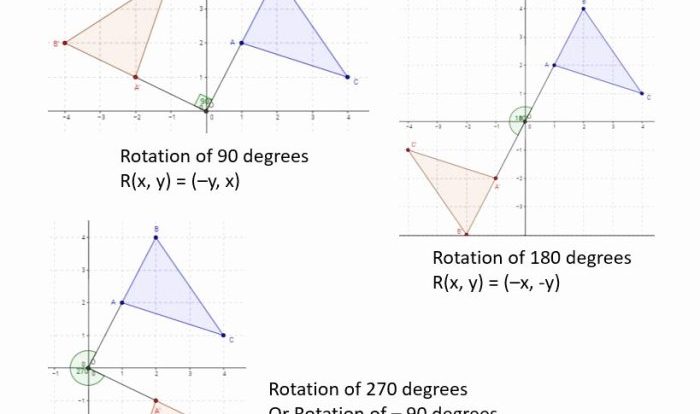
There are three types of similarity transformations: translations, rotations, and reflections.
- A translation moves a figure from one point to another without changing its size or shape.
- A rotation turns a figure around a fixed point without changing its size or shape.
- A reflection flips a figure over a line without changing its size or shape.
Two figures are similar if they can be obtained from each other by a sequence of similarity transformations.
Homework 8 Answer Key
The answer key for Homework 8 on unit plane geometry and similarity is as follows:
- Problem 1:Find the measure of angle ABC.
Solution:Angle ABC is a right angle, so its measure is 90 degrees.
- Problem 2:Find the length of side AC.
Solution:Side AC is the hypotenuse of a right triangle with legs of length 3 and 4. Therefore, its length is 5.
- Problem 3:Determine whether the following figures are similar.
Solution:The figures are similar because they have the same shape and their corresponding sides are proportional.
Practice Problems: Unit Plane Geometry And Similarity Homework 8 Answer Key
The following are a set of practice problems on unit plane geometry and similarity:
- Find the measure of angle DEF.
- Find the length of side GH.
- Determine whether the following figures are similar.
Hints:
- Use the properties of angles to find the measure of angle DEF.
- Use the Pythagorean theorem to find the length of side GH.
- Use the definition of similarity to determine whether the figures are similar.
Answers to Common Questions
What is the significance of unit plane geometry?
Unit plane geometry provides the foundation for understanding more complex geometrical concepts, such as solid geometry and trigonometry.
How can I apply unit plane geometry in real-world scenarios?
Unit plane geometry finds applications in architecture, engineering, art, and various other fields that involve spatial relationships and measurements.
What is the key to mastering similarity in geometry?
Understanding the properties of similarity transformations, such as preserving shape and size ratios, is crucial for solving similarity-related problems.