Unveiling the mysteries of geometry, the Angle Relationships Worksheet 2 Answer Key emerges as an indispensable guide, illuminating the intricacies of angle relationships and empowering students to conquer geometric challenges with confidence.
This comprehensive resource delves into the fundamental concepts of angle relationships, providing a structured approach to understanding supplementary, complementary, vertical, and adjacent angles. With clear explanations, illustrative examples, and practical problem-solving techniques, this answer key serves as an invaluable tool for students seeking to master the art of geometry.
Angle Relationships Worksheet 2 Key Overview
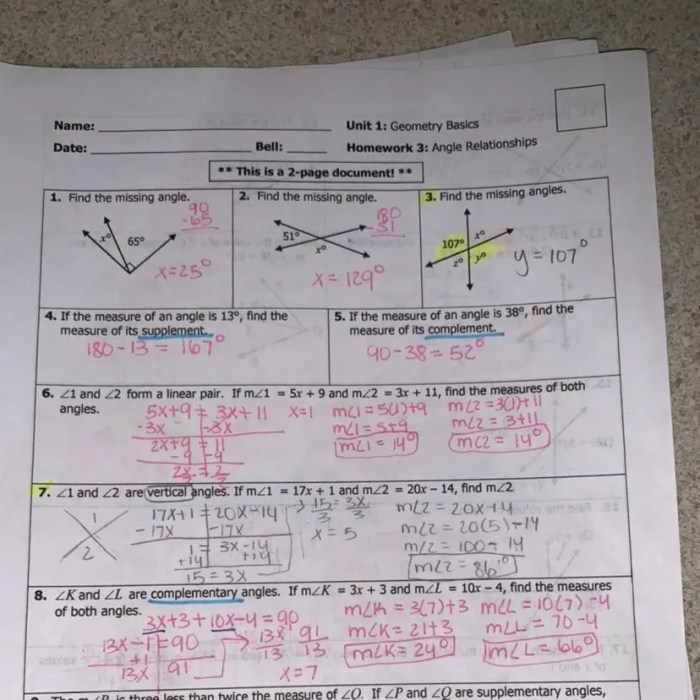
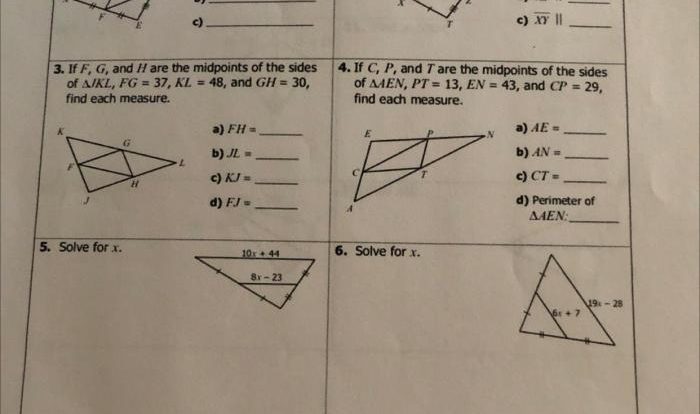
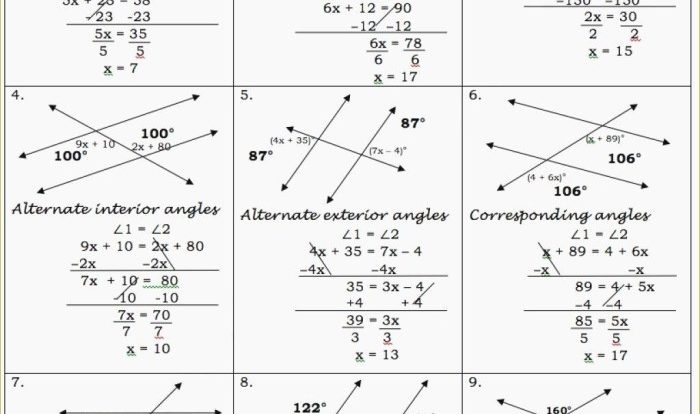
The Angle Relationships Worksheet 2 is designed to help students practice identifying and classifying different types of angle relationships. It covers concepts such as supplementary angles, complementary angles, vertical angles, and adjacent angles, as well as angle sum properties of triangles and quadrilaterals.
Supplementary Angle Relationships
Supplementary angles are two angles that add up to 180 degrees. To identify supplementary angles in the worksheet, look for pairs of angles that are adjacent and form a straight line.
Examples:
- ∠A and ∠B in the triangle
- ∠C and ∠D in the quadrilateral
Complementary Angle Relationships, Angle relationships worksheet 2 answer key
Complementary angles are two angles that add up to 90 degrees. To identify complementary angles in the worksheet, look for pairs of angles that are adjacent and form a right angle.
Examples:
- ∠E and ∠F in the triangle
- ∠G and ∠H in the quadrilateral
Vertical Angle Relationships
Vertical angles are two angles that are opposite each other when two lines intersect. To identify vertical angles in the worksheet, look for pairs of angles that share a common vertex and are not adjacent.
Examples:
- ∠I and ∠J
- ∠K and ∠L
Adjacent Angle Relationships
Adjacent angles are two angles that share a common side and a common vertex. To identify adjacent angles in the worksheet, look for pairs of angles that are next to each other and do not overlap.
Examples:
- ∠A and ∠B in the triangle
- ∠C and ∠D in the quadrilateral
Angle Sum Properties
The angle sum properties state that the sum of the interior angles of a triangle is 180 degrees and the sum of the interior angles of a quadrilateral is 360 degrees. To apply these properties in the worksheet, use them to find the measure of an unknown angle when given the measures of the other angles in the figure.
Examples:
- In the triangle, if ∠A = 60° and ∠B = 70°, then ∠C = 50° (180° – 60° – 70°).
- In the quadrilateral, if ∠E = 90°, ∠F = 100°, and ∠G = 120°, then ∠H = 50° (360° – 90° – 100° – 120°).
Solving for Unknown Angles
To solve for unknown angles in the worksheet, use the angle relationships and angle sum properties discussed above. Consider the following strategies:
- Use the definition of supplementary, complementary, vertical, or adjacent angles to find the measure of one angle if given the measure of the other.
- Use the angle sum properties to find the measure of an unknown angle when given the measures of the other angles in the figure.
- Use algebraic techniques, such as solving equations, to find the measure of an unknown angle.
Quick FAQs: Angle Relationships Worksheet 2 Answer Key
What is the purpose of the Angle Relationships Worksheet 2?
The Angle Relationships Worksheet 2 aims to enhance students’ understanding of various angle relationships, including supplementary, complementary, vertical, and adjacent angles.
How can I identify supplementary angles in the worksheet?
Supplementary angles are two angles that sum up to 180 degrees. To identify them, look for pairs of angles that are adjacent and form a straight line.
What is the definition of vertical angles?
Vertical angles are two angles that are formed by two intersecting lines and are opposite each other. They are always congruent, meaning they have the same measure.