Delving into the intricacies of proving lines parallel, this comprehensive guide unveils the fundamental concepts, diverse methods, and practical applications that underpin this geometrical principle. Through a meticulous exploration of proving lines parallel worksheet answers, we embark on a journey to illuminate the complexities of parallel lines and their significance in shaping our understanding of geometry.
The ensuing paragraphs delve into the theoretical foundations of parallel lines, examining their defining characteristics and the various techniques employed to establish their parallelism. By scrutinizing the provided worksheet answers, we uncover the step-by-step procedures involved in proving lines parallel, reinforcing our comprehension of this geometrical concept.
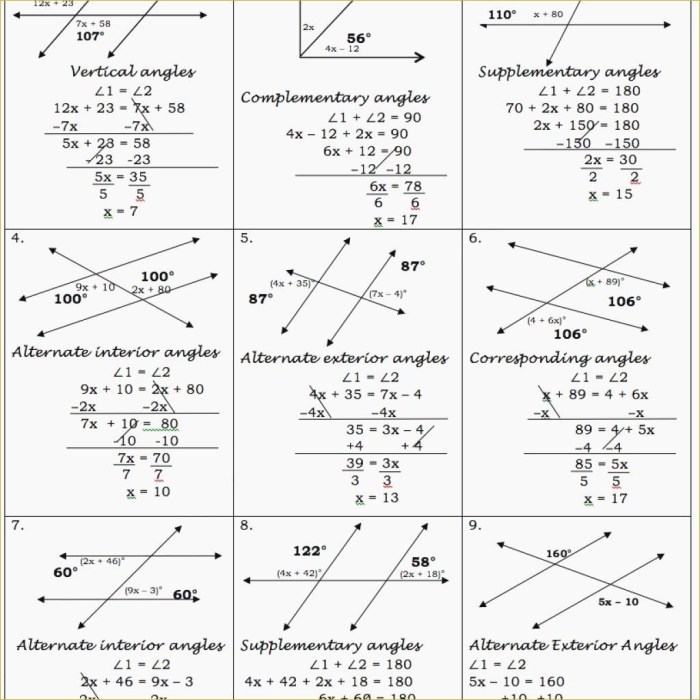
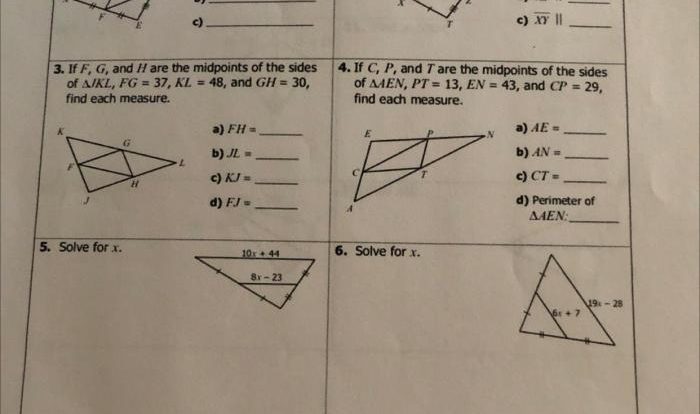
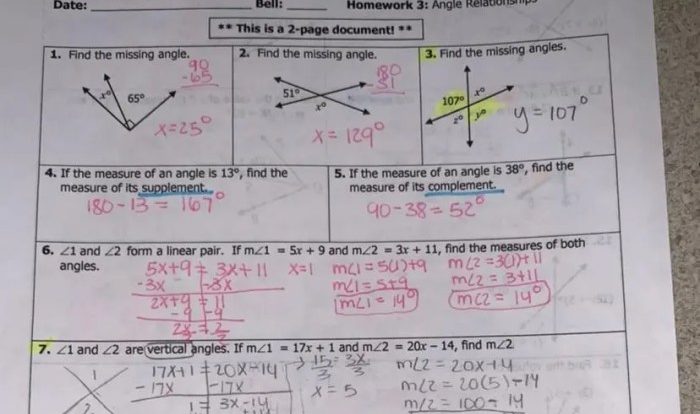
Proving Lines Parallel
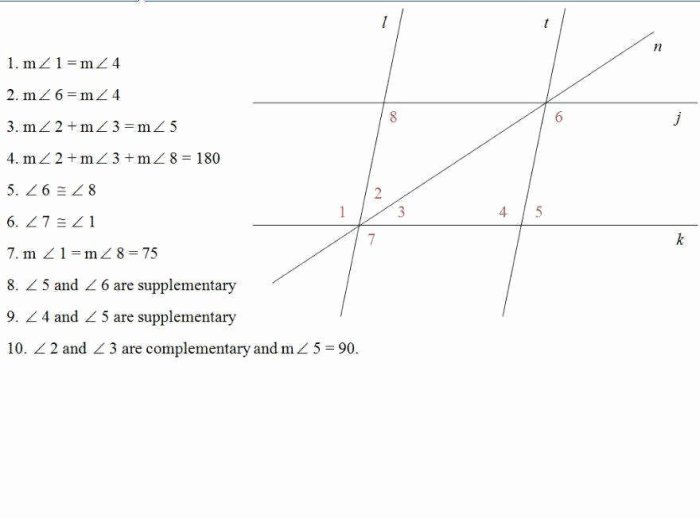
In geometry, parallel lines are two lines that never intersect, no matter how far they are extended. There are several different methods for proving that two lines are parallel, including:
Angle Relationships, Proving lines parallel worksheet answers
- If two lines are cut by a transversal and the alternate interior angles are congruent, then the lines are parallel.
- If two lines are cut by a transversal and the same-side interior angles are supplementary, then the lines are parallel.
- If two lines are cut by a transversal and the alternate exterior angles are congruent, then the lines are parallel.
Slope
If two lines have the same slope, then they are parallel.
Intercepts
If two lines have different intercepts, then they are parallel.
Worksheet Answers: Proving Lines Parallel Worksheet Answers
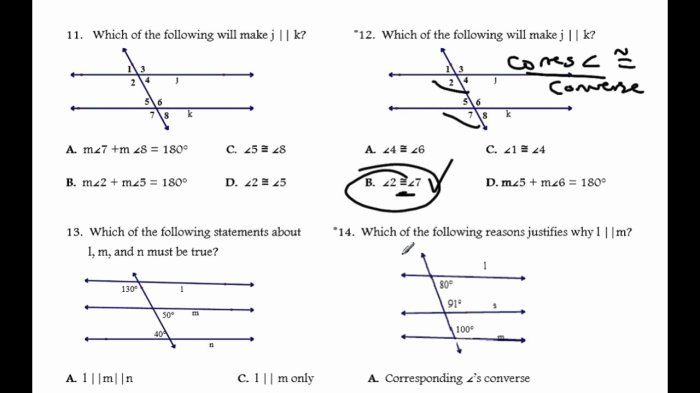
| Problem | Method of Proof | Answer |
|---|---|---|
| Prove that lines l and m are parallel. | Angle Relationships (Alternate Interior Angles) |
Given: ∠1 ≅ ∠3 Prove: l|| m Proof: Since ∠1 ≅ ∠3, then land mare cut by a transversal and the alternate interior angles are congruent. Therefore, by the Alternate Interior Angles Theorem, l|| m. |
| Prove that lines n and p are parallel. | Slope |
Given: n: y= 2 x+ 1 p: y= 2 x– 3 Prove: n|| p Proof: The slope of line nis 2, and the slope of line pis also 2. Since the slopes are equal, nand pare parallel. |
| Prove that lines q and r are parallel. | Intercepts |
Given: q: y= 3 r: y= -2 Prove: q|| r Proof: The y-intercept of line qis 3, and the y-intercept of line ris -2. Since the y-intercepts are different, qand rare parallel. |
FAQs
What is the definition of parallel lines?
Parallel lines are coplanar lines that never intersect, no matter how far they are extended.
What are the different methods for proving lines parallel?
There are several methods for proving lines parallel, including the use of alternate interior angles, corresponding angles, and the slope of the lines.
What are some common applications of proving lines parallel?
Proving lines parallel has numerous applications in architecture, engineering, and design, where it is essential for ensuring the structural integrity and aesthetic appeal of various constructions.