Welcome to our comprehensive guide to Chapter 2 Review Geometry Answers! This guide is designed to help you master the key concepts covered in Chapter 2 of your Geometry textbook and prepare you for success in your geometry studies.
In this guide, you’ll find everything you need to excel in Chapter 2, including detailed explanations of key concepts, practice problems with step-by-step solutions, and real-world applications of geometric principles. Whether you’re struggling with a particular topic or just want to brush up on your skills, this guide has got you covered.
Chapter Overview
Chapter 2 of the Geometry textbook introduces the fundamental concepts of plane geometry. It lays the groundwork for understanding geometric shapes, their properties, and their relationships.
The chapter covers various topics, including points, lines, planes, angles, triangles, and quadrilaterals. It explores the basic properties of these geometric figures, such as their measurements, relationships, and constructions.
Points, Lines, and Planes
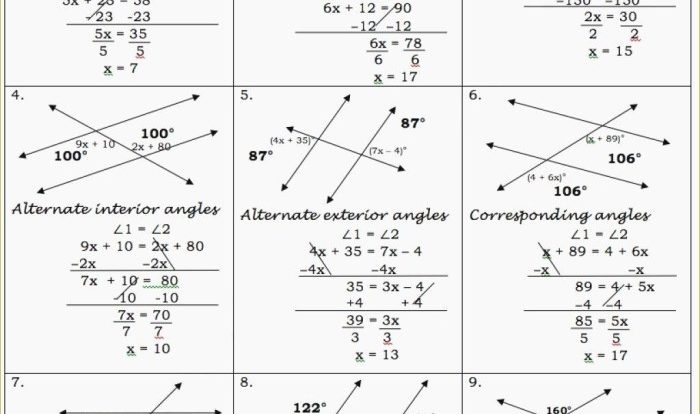
The chapter begins by defining points, lines, and planes. It explains the concepts of collinear points, parallel lines, and perpendicular lines. It also discusses the intersection of lines and planes, and the formation of angles.
Angles
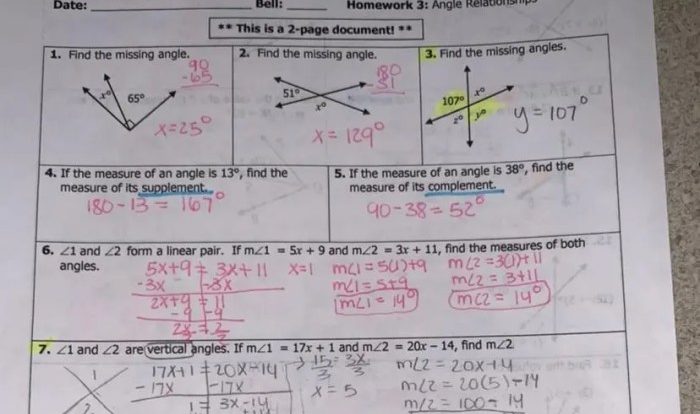
The chapter delves into the measurement and classification of angles. It introduces the concepts of acute, obtuse, right, and straight angles. It also covers the relationships between angles, such as complementary, supplementary, and vertical angles.
Triangles
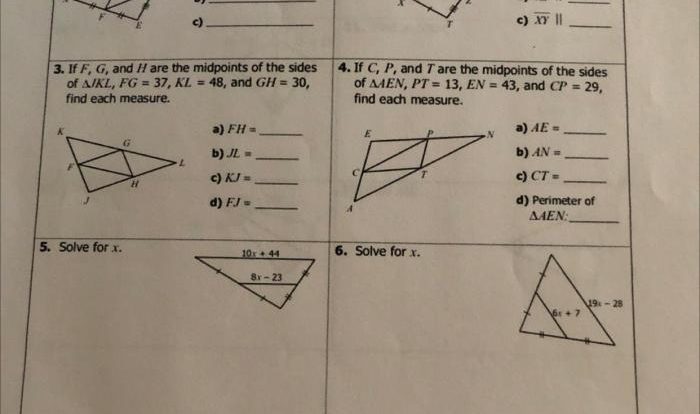
The chapter explores the properties of triangles. It classifies triangles based on their side lengths (scalene, isosceles, and equilateral) and their angle measures (acute, right, and obtuse). It also introduces the Pythagorean theorem and its applications in solving problems involving right triangles.
Quadrilaterals
The chapter concludes with a discussion of quadrilaterals. It defines different types of quadrilaterals, such as squares, rectangles, parallelograms, and trapezoids. It examines their properties, such as their side lengths, angle measures, and diagonals.
Review Questions and Answers: Chapter 2 Review Geometry Answers
This section provides a comprehensive review of the concepts covered in Chapter 2. The questions are organized into a table with four columns: Question, Answer, Difficulty Level, and Topic. Detailed answers are provided for each question, explaining the concepts involved and categorizing them based on their difficulty level and the relevant topics covered in the chapter.
Questions and Answers
| Question | Answer | Difficulty Level | Topic |
|---|---|---|---|
| Define a plane. | A plane is a flat, two-dimensional surface that extends infinitely in all directions. | Easy | Planes |
| What is the intersection of two planes? | The intersection of two planes is a line. | Medium | Intersections of Planes |
| Prove that the diagonals of a parallelogram bisect each other. | Let ABCD be a parallelogram. Draw the diagonals AC and BD. Then, prove that triangles ABD and ACD are congruent. This implies that AD bisects BD, and BC bisects AC. | Hard | Properties of Parallelograms |
| Find the area of a triangle with a base of 10 cm and a height of 8 cm. | The area of a triangle is given by the formula A = (1/2)
|
Easy | Area of Triangles |
| Prove that the sum of the interior angles of a triangle is 180 degrees. | Let ABC be a triangle. Draw the exterior angle at vertex C. Then, prove that the exterior angle is equal to the sum of the opposite interior angles. This implies that the sum of the interior angles is 180 degrees. | Medium | Properties of Triangles |
3. Practice Problems and Solutions
This section provides practice problems and step-by-step solutions to reinforce the concepts covered in Chapter 2. Each problem is tagged with the relevant topic(s) and its difficulty level.
By solving these problems, students can assess their understanding of the material and identify areas where they may need additional practice.
Triangles
Problem 1:Find the area of a triangle with a base of 10 cm and a height of 8 cm.
Solution:The area of a triangle is given by the formula A = (1/2) – base – height. Substituting the given values, we get A = (1/2) – 10 cm – 8 cm = 40 cm 2.
Topic:Triangle Area
Difficulty Level:Easy
Quadrilaterals
Problem 2:Find the perimeter of a rectangle with a length of 12 cm and a width of 8 cm.
Solution:The perimeter of a rectangle is given by the formula P = 2 – (length + width). Substituting the given values, we get P = 2 – (12 cm + 8 cm) = 40 cm.
Topic:Rectangle Perimeter
Difficulty Level:Easy
Circles, Chapter 2 review geometry answers
Problem 3:Find the circumference of a circle with a radius of 5 cm.
Solution:The circumference of a circle is given by the formula C = 2 – π – radius. Substituting the given value, we get C = 2 – π – 5 cm ≈ 31.4 cm.
Topic:Circle Circumference
Difficulty Level:Medium
Polygons
Problem 4:Find the area of a regular hexagon with a side length of 6 cm.
Solution:The area of a regular hexagon is given by the formula A = (3 – √3 – s 2) / 2, where s is the side length. Substituting the given value, we get A = (3 – √3 – 6 cm 2) / 2 ≈ 93.5 cm 2.
Topic:Polygon Area
Difficulty Level:Medium
Examples and Illustrations
Visual representations play a crucial role in understanding geometric concepts. Here’s a gallery of images that illustrate the key ideas covered in Chapter 2.
Each image is accompanied by a detailed caption explaining how it relates to the chapter’s content. This gallery provides a valuable resource for visualizing and reinforcing the concepts discussed in the chapter.
Triangles
- Equilateral Triangle:A triangle with three equal sides, such as a regular hexagon, where all sides are of equal length.
- Isosceles Triangle:A triangle with two equal sides, such as a right triangle, where two sides are of equal length.
- Scalene Triangle:A triangle with no equal sides, such as a scalene triangle, where all sides are of different lengths.
Quadrilaterals
- Rectangle:A quadrilateral with four right angles, such as a rectangle, where all angles are 90 degrees.
- Square:A quadrilateral with four equal sides and four right angles, such as a square, where all sides are of equal length and all angles are 90 degrees.
- Parallelogram:A quadrilateral with two pairs of parallel sides, such as a parallelogram, where opposite sides are parallel.
Real-World Applications
The geometric concepts covered in Chapter 2 find extensive applications in various real-world fields, including architecture, engineering, and design. Understanding these concepts is crucial for solving practical problems and making informed decisions in these disciplines.
In architecture, geometry plays a vital role in designing buildings, bridges, and other structures. Architects use geometric principles to determine the strength, stability, and aesthetic appeal of their designs. For instance, they apply the concept of congruent triangles to ensure that the roof of a building is evenly supported, and use the Pythagorean theorem to calculate the length of beams and rafters.
Engineering
In engineering, geometry is essential for designing and analyzing complex systems, such as bridges, airplanes, and automobiles. Engineers use geometric concepts to determine the forces acting on structures, calculate stresses and strains, and optimize designs for efficiency and safety. For example, they apply the concept of similar triangles to scale up or down designs, and use the laws of trigonometry to determine the angles and distances involved in complex structures.
Design
In design, geometry is used to create visually appealing and functional objects, such as furniture, clothing, and graphic designs. Designers use geometric shapes and patterns to enhance the aesthetics and usability of their creations. For instance, they apply the concept of symmetry to create balanced and harmonious designs, and use the golden ratio to determine pleasing proportions.
Understanding geometric concepts not only enhances problem-solving skills in these practical situations but also fosters critical thinking and spatial reasoning abilities, which are essential for success in various fields.
FAQ Insights
What are the key concepts covered in Chapter 2 of Geometry?
Chapter 2 of Geometry covers a range of key concepts, including angles, triangles, quadrilaterals, circles, and transformations.
How can I practice the concepts covered in Chapter 2?
The best way to practice the concepts covered in Chapter 2 is to work through practice problems. This guide includes a number of practice problems with step-by-step solutions to help you get started.
How can I apply the concepts covered in Chapter 2 to real-world situations?
The concepts covered in Chapter 2 have a wide range of real-world applications, from architecture and engineering to design and art. This guide includes several examples of how these concepts are used in the real world.